Nombres impairs Le nombre impair ne peut pas être divisé de manière égale car l'unité, soit 1, reste toujours indivisible.
Par exemple :
9 = 4 + 1 + 4
19 = 9 + 1 + 9
153 = 76 + 1 + 76…etc.
Il est utile de commencer à voir les nombres impairs de cette façon. Chaque nombre impair tourne autour de l’axe central de l’unité. Bien que le nombre soit séparé ou fracturé, il conserve son lien avec l’unité. En fait, ses parties tourbillonnent continuellement autour de l’unité comme l’eau tourbillonne autour d’un égout, ou comme un chien qui court après sa queue, en tournant en rond et dans le cas des nombres, sans jamais s’arrêter. Cela lui donne une qualité de mouvement et d’action – d’où sa représentation par le principe masculin actif.
De plus, si un nombre impair est divisé en deux parties, une partie sera toujours impaire et l’autre paire.
Par exemple :
9 = 4 + 5
19 = 9 + 10
153 = 76 + 77…etc.
Nombres pairs Le nombre pair peut être divisé en deux parties égales, qui sont toujours soit toutes les deux impaires, soit toutes les deux paires
Par exemple :
10 = 5 + 5
144 = 72 + 72
360 = 180 + 180
Vous pouvez voir comment les nombres pairs contiennent la qualité de passivité. Ils sont égaux et statiques. Ils ne contiennent pas le mouvement inhérent aux nombres impairs qui tourbillonnent continuellement pour essayer d'équilibrer leurs parties. Par conséquent, les nombres pairs représentent le principe féminin passif.

Classes de nombres impairs Il existe trois classes générales de nombres impairs : les nombres non composés, les nombres composés et les nombres non composés-composites. Les nombres non composés sont des nombres premiers. Ils n'ont pas d'autre diviseur qu'eux-mêmes et l'unité. Par exemple : 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41…etc. Lisez l'article 9 pour plus d'informations sur les nombres premiers. Les nombres composés sont divisibles non seulement par eux-mêmes et l'unité, mais aussi par un autre nombre. Exemples : 9, 15, 21, 25, 27, 33, 39, 45, 51, 57…etc. 15 est divisible par 15 et 1 mais aussi par 3 et 5. 39 est divisible par 39 et 1 mais aussi par 3 et 13. 57 est divisible par 57 et 1 mais aussi par 3 et 19. Les nombres incomposites-composites n'ont pas de diviseur commun, bien que chacun d'eux soit divisible, comme 9 et 25. Cela signifie qu'ils sont divisibles par eux-mêmes et par l'unité, ainsi que par un seul autre nombre. Parce qu'ils ont des diviseurs individuels, on les appelle composés. Parce qu'ils n'ont pas de diviseur commun (comme le 3 commun ci-dessus), on les appelle incomposites.
Classes de nombres pairs Il existe trois classes générales de nombres pairs : pair-pair, pair-impair et impair-pair. Les nombres pair-pair sont tous en raison double à partir de l'unité. Ces nombres peuvent être divisés par deux, puis à nouveau par deux jusqu'à l'unité.
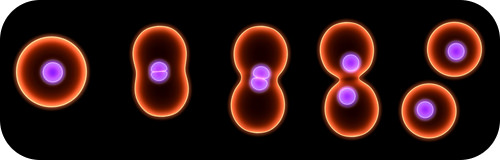
Par exemple : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024…etc. Ex. 128/2 = 64 ; 64/2 = 32 ; 32/2 = 16 ; 16/2 = 8 ; 8/2 = 4 : 4/2 = 2 ; 2/2 = 1 Les nombres pairs possèdent certaines propriétés uniques. La somme de n’importe quel nombre de termes, à l’exception du dernier terme, est toujours égale au dernier terme moins un. Par exemple : La somme des 2 premiers termes (1 + 2 = 3) est égale au troisième terme (4) moins 1 (3), ou : La somme des 1er, 2e, 3e et 4e termes (1 + 2 + 4 + 8 = 15) est égale au 5e terme (16) moins 1 (15). La somme des termes 1 à 10 = 1023. Cela équivaut au 11e terme (1024) moins 1 = 1023. Ceci s’applique à tous les termes de cette série. Cette série pair-pair représente le processus de dédoublement observé dans la division cellulaire et la structure des octaves. N’oubliez pas que les nombres ne sont pas des « choses » statiques. Ils représentent des processus. Les nombres pair-impair sont des nombres qui, une fois divisés par deux, ne peuvent plus être divisés par deux. On les forme en prenant les nombres impairs dans l'ordre séquentiel et en les multipliant par 2. Les nombres impairs 1, 3, 5, 7, 9, 11 produisent les nombres pair-impairs 2, 6, 10, 14, 18, 22. En commençant par 2, un nombre sur quatre est pair-impair. Le nombre à diviser est le dividende. Le nombre qui divise est le diviseur. Le résultat de la division est le quotient.
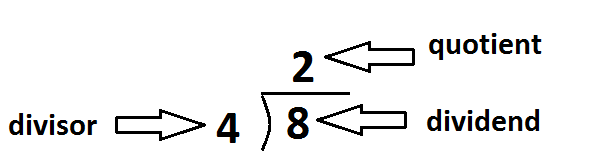
Par exemple : dans 360/6 = 60, 360 est le dividende. 6 est le diviseur. 60 est le quotient. Si le diviseur est impair, le quotient est toujours pair. Par exemple : 18/3 (diviseur impair) = 6 (quotient pair) Si le diviseur est pair, le quotient est toujours impair. Par exemple : 18/2 (diviseur pair) = 9 (quotient impair) De plus, chaque terme de la série est la moitié de la somme des termes de chaque côté. Par exemple : 10 est la moitié de la somme des termes de chaque côté (14 + 6 = 20). 18 est la moitié de la somme des termes de chaque côté (22 + 14 = 36)…etc. Les nombres impairs-impairs ou inégalement-pairs sont un compromis entre les nombres uniformément pairs et les nombres uniformément impairs. Contrairement aux nombres pair-pair, ils ne peuvent pas être divisés par deux jusqu'à l'unité ; et contrairement aux nombres impairs-pairs, ils sont capables de plus d'une division par deux. Par exemple : 24 24 /2 = 12 12/2 = 6 6/2 = 3 Trois autres classes de nombres pairs Il existe trois autres classes de nombres pairs : les superparfaits, les déficients et les parfaits. Les nombres superparfaits ont la somme de leurs parties fractionnaires supérieure à eux-mêmes. Par exemple : Le nombre 24 : ½ de 24 = 12 ; ¼ de 24 = 6 ; 1/3 de 24 = 8 ; 1/6 de 24 = 4 ; 1/12 de 24 = 2 ; 1/24 = 1 La somme de ces parties (12 + 6 + 8 + 4 + 2 + 1) = 33 ; qui est supérieur à 24. Les nombres déficients sont des nombres dont la somme de leurs parties fractionnaires est inférieure à elle-même. Par exemple :
Le nombre 14 : ½ de 14 = 7 ; 1/7 de 14 = 2 ; 1/14 = 1 La somme des parties (7 + 2 + 1) = 10, ce qui est inférieur à 14. Les nombres parfaits sont ceux dont la somme de leurs parties fractionnaires est égale à elle-même. Par exemple : Le nombre 28 : ½ de 28 = 14 ; ¼ de 28 = 7 ; 1/7 de 28 = 4 ; 1/14 de 28 = 2 ; 1/28 = 1 La somme des parties (14 + 7 + 4 + 2 + 1) = 28, ce qui est égal à 28. Les nombres parfaits sont extrêmement rares. Il n'y en a qu'un entre 1 et 10 = 6 Un entre 10 et 100 = 28 Un entre 100 et 1000 = 496 Un entre 1000 et 10000 = 8128 Le cinquième nombre parfait = 33550336 « Les nombres parfaits sont de belles images des vertus qui sont des intermédiaires certains entre l'excès et le défaut. Au contraire, on peut trouver une multitude infinie de nombres surabondants et diminués, qui ne sont ni disposés en une série ordonnée ni engendrés par une fin certaine ; et par conséquent ils ont une grande similitude avec les vices, qui sont nombreux, déréglés et indéfinis. » Thomas Taylor, Arithmétique théorique La théorie des nombres des mathématiques pythagoriciennes est peut-être l’une des informations les plus sèches incluses dans le projet de thèse Cosmic Core, mais elle est incluse parce qu’elle est nécessaire pour comprendre l’importance profonde que le nombre avait dans la philosophie ancienne et ésotérique et comment les nombres étaient considérés non pas comme des quantités, mais comme des symboles contenant diverses qualités. Ces qualités du nombre étaient comparées aux qualités de nos pensées, de nos émotions et de nos actions.
Pour toute pensée, émotion ou action, vous pouvez contempler ses qualités. Contient-elle de l’harmonie ? Vous apporte-t-elle la paix ? Vous met-elle en colère ? Vous fait-elle sentir supérieur ? Inférieur ? Vous donne-t-elle envie de faire du mal à quelqu’un ou à vous-même ? Vous donne-t-elle envie d’aider ? Vous fait-elle sentir puissant ? Impuissant ? Craintif ? Confiant ? Jaloux ? Compatissant ? Confus ? Élevé ? Le fait de remettre en question vos croyances, vos pensées, vos émotions et vos actions au fur et à mesure qu’elles se produisent est la leçon la plus importante à tirer de ces informations. Quelles pensées nous ramènent vers l’unité et quelles pensées nous séparent des autres ou de nous-mêmes ? À quel point ces pensées sont-elles proches de l’unité et à quelle distance ? Les nombres sont des symboles de ces attributs de notre conscience – nos pensées, nos émotions, nos croyances, nos attentes et nos actions. Les nombres parfaits sont considérés comme ces vertus divines – ces pensées et intentions pures et altruistes qui nous ramènent directement à l’unité – des pensées, des émotions et des actions qui contiennent un équilibre parfait de sagesse et de compassion, d’action et de passivité, de force et de douceur.

Gnomons « Pythagore enseignait que l’expérience de la vie dans un corps fini et limité avait pour but spécifique de découvrir et de manifester l’existence surnaturelle au sein du fini. La concentration doit donc également être sur le fini lui-même, pour découvrir comment ce fini pourrait contenir intrinsèquement un pouvoir d’exprimer l’infini. Cela ne signifie pas se concentrer sur des effets finis et matériels, mais sur les principes abstraits révélés dans le monde fini et les causes qui créent et soutiennent cette incarnation. Par conséquent, les mathématiques pythagoriciennes se limitaient aux nombres entiers, c’est-à-dire aux états définissables et arrêtés, et recherchaient des expressions universelles avec le cadre géométrique mesurable du carré, un symbole profond de la perfection finie. » – Robert Lawlor, Géométrie sacrée : philosophie et pratique

La croissance gnomonique est toute figure qui, lorsqu'elle est ajoutée à une autre figure, laisse la figure résultante semblable à l'originale. Ceci est lié à l'invariance d'échelle, ou auto-similarité fractale, qui a été abordée dans l'article 2 et sera abordée beaucoup plus en détail dans les prochains articles. « Certaines choses ne subissent aucun changement autre que de grandeur lorsqu'elles grandissent » : c'est le principe de la croissance gnomonique ou de l'invariance d'échelle.


Nous allons aborder brièvement les nombres gnomoniques relatifs aux mathématiques pythagoriciennes, en rappelant que les philosophes antiques tels que Pythagore, Platon et Euclide n'avaient pas de chiffres à disposition, mais utilisaient de petits cailloux pour étudier les nombres. En utilisant cette méthode, il est beaucoup plus facile de voir la nature géométrique des nombres. Nombres triangulaires Les nombres triangulaires augmentent de manière triangulaire, comme 1, 3, 6, 10, 15, 21…etc.
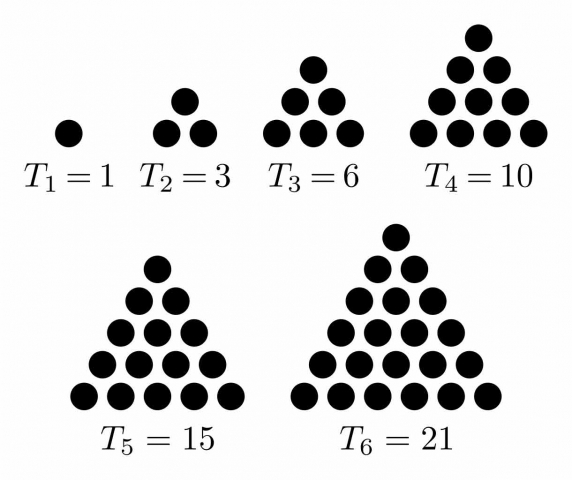
Un nombre triangulaire est constitué de tous les nombres depuis l'unité jusqu'à une limite donnée. La série qu'ils forment est la suivante : 3 (= 1 + 2) 6 (= 1 + 2 + 3) 10 (= 1 + 2 + 3 + 4) 15 (= 1 + 2 + 3 + 4 + 5) 21 (= 1 + 2 + 3 + 4 + 5 + 6) et ainsi de suite. Lorsqu'ils sont disposés à l'aide de cailloux, ils forment des triangles. Nombres rectangulaires Les nombres rectangulaires augmentent de manière musicale en fonction des octaves, comme 2, 6, 12, 20. Lorsqu'ils sont disposés à l'aide de cailloux, ils forment des rectangles.
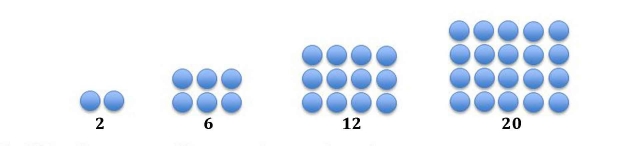
Nombres carrés Les nombres carrés sont constitués de deux nombres triangulaires successifs, tels que 1, 4, 9, 16.

Par exemple : 4 = 1 + 3 9 = 6 + 3 16 = 10 + 6…etc. Ces nombres sont les « carrés » littéraux de nombres : 22 = 4 32 = 9 42 = 16 52 = 25…etc. Disposés à l’aide de cailloux, ils forment des carrés. Nombres cubiques Les nombres cubiques sont les « cubes » littéraux de nombres, tels que 1, 8, 27, 64, 125…etc.
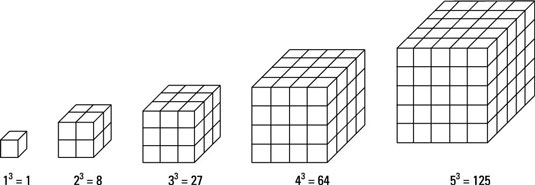
Par exemple : 23 = 8 33 = 27 43 = 64 53 = 125 Lorsqu'ils sont disposés en trois dimensions à l'aide de galets, ils forment des cubes. Le Lambda Le Lambda est une figure numérique-géométrique qui a été étudiée par les Grecs de l'Antiquité. Elle a été décrite par Platon dans le Timée comme « l'âme du monde ».

Platon affirme que Dieu a créé l’âme cosmique en utilisant deux bandes mathématiques de 1, 2, 4, 8 et 1, 3, 9, 27. Ces deux bandes suivent la forme d’un « V » inversé ou le « Lambda platonicien ». Lambda est la 11e lettre de l’alphabet grec. Elle est de nature triangulaire, comme la tétraktys discutée ci-dessous. La forme triangulaire représente sa nature divine. « Platon considère que la proportion géométrique continue est le lien cosmique le plus profond. Dans son Timée, l’âme du monde lie en une résonance harmonique le monde intelligible des formes (y compris les mathématiques pures) au-dessus, et le monde visible des objets matériels au-dessous, à travers les séries 1, 2, 4, 8 et 1, 3, 9, 27. »2 Le résultat de l’âme du monde de Platon est le Lambda – une proportion géométrique continue étendue.
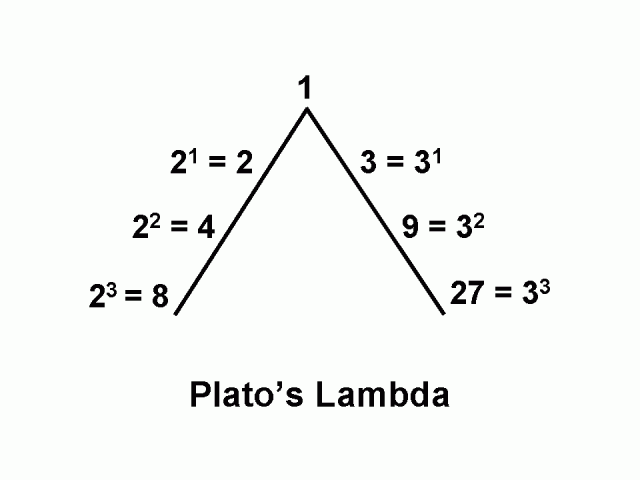
La première série : 1, 2, 4, 8 est la séquence de doublement. Comme nous l’avons vu plus haut, les nombres pairs sont associés au principe féminin passif. La deuxième série : 1, 3, 9, 27 est la séquence de triplement. Ces nombres impairs sont associés au principe masculin actif. Ces deux séries produisent ensemble toute la gamme des rapports musicaux, c’est-à-dire l’octave (2:1), la quinte (3:2), la quarte (4:3) et le ton entier (9:8). Nous en discuterons en détail dans des articles ultérieurs. Robert Lawlor explique : « Dans la progression arithmétique, l’addition est le moyen de croissance, tandis que dans la progression dite « géométrique » (dont un exemple est 2, 4, 8, 16…) chaque terme successif se déploie en étant multiplié par le premier terme. Ainsi, l’addition et la multiplication restent nos deux métaphores mathématiques les plus efficaces pour décrire la croissance organique d’une part et l’accumulation physique ou gnomonique d’autre part.
The type of progression, which combines both the additive and multiplicative growth procedures of the other two progressions, is called ‘harmonic’. The most important and mysterious characteristic of this form of harmonic, proportional progression is the fact that the inverse of any harmonic progression is an arithmetic progression. Thus 2, 3, 4, 5…is an ascending arithmetic progression, while the inverse series (1/2, 1/3, ¼, 1/5…) is a descending harmonic progression.
These two parallel yet inversing progressions not only provide the foundations of music, but more generally provide a mathematical model with which to investigate the complementary or opposed symmetries of dualized, yet harmonically integrated, whole. For this reason the musical metaphor was the cornerstone of ancient philosophy, applicable to both physical and metaphysical domains.”
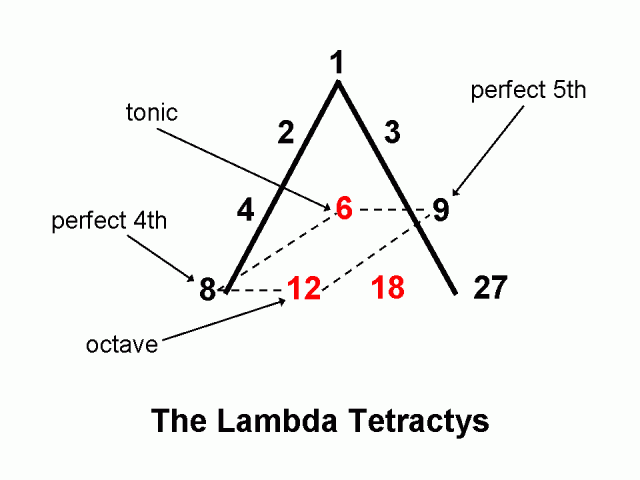
Robert Lawlor nous dit : « On attribue à Pythagore le mérite d’avoir établi le premier la relation entre les rapports numériques et les fréquences sonores. Les rapports de nombres entiers permettant de déterminer les consonnes dans une gamme musicale sont soit tirés des nombres des deux progressions du Lambda, soit en sont des multiples. » « L’intention évidente de Platon », déclare John Michell à propos du Lambda, « était d’identifier le nombre comme l’archétype de la création et d’attirer l’attention sur ces nombres particuliers qui constituent son noyau et qui, dans diverses combinaisons, génèrent l’ensemble du champ du nombre. »

Le Tétraktys Le Tétraktys est une autre figure numérique-géométrique associée à l'école pythagoricienne. Nous l'avons mentionné dans des articles précédents. Freddy Silva écrit : « Bien qu'attribuée à Pythagore, la tétractys peut être retracée jusqu'aux hindous, et avant eux, c'est une question de conjecture. Comme la Fleur de Vie, ce qui est certain, c'est l'association de cette figure avec le processus créatif. Théon de Smyrne, un érudit renommé de l'Antiquité, a déclaré que les dix points de la tétractys représentaient les dix paroles de Dieu. Pour les chrétiens, ces « mots » signifiaient les dix commandements ; pour les hébreux, les dix sphères de l'arbre de vie. Cependant, le symbolisme numérique de la tétractys correspond également au modèle hindou des neuf cobras autour de Brahma, de la Grande Ennéade égyptienne autour d'Atoum et des neuf légions d'angles kabbalistiques autour du Dieu caché. » Il est constitué de dix points disposés en triangle équilatéral. Comme dans le Lambda, la forme triangulaire représente sa nature divine.
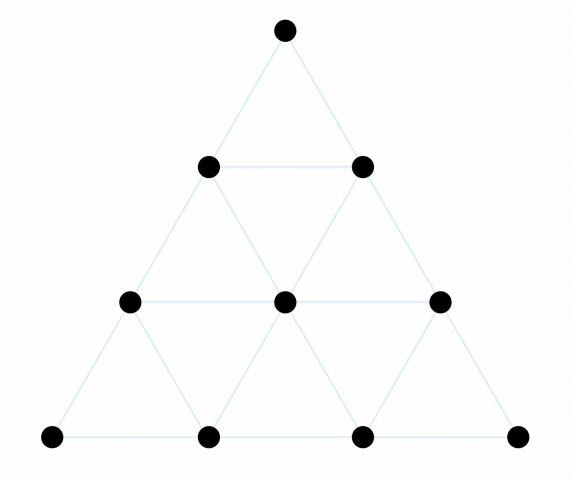
Le tétraktys est un « modèle cosmologique basé sur la complétude de dix points se déployant sur quatre niveaux pour décrire le processus de création universel. »3 Le tétraktys est une représentation de la Décade – les nombres de 1 à 10. Il se compose de 4 niveaux. Notez que 10 = 1 + 2 + 3 + 4. Les quatre niveaux représentent les densités croissantes des 4 éléments : la terre (le plus dense), l'eau, l'air et le feu (le moins dense).

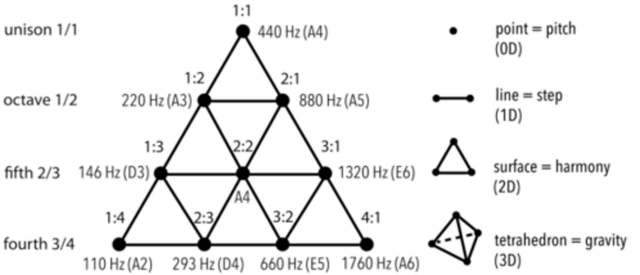
Les quatre niveaux font également référence aux différentes perspectives de vision de tout sujet :

Les quatre niveaux font également référence aux quatre niveaux de connaissance. Ils sont les suivants : • Données sensorielles : « une multiplicité déroutante de visions, de sons, de sensations, d’odeurs, de goûts, etc., une pure différence ». • Reconnaissance : acquérir des informations • Connaissance : la capacité de reconnaître ou de distinguer et de convenir de connaissances partagées afin d’établir la vérité. • Sagesse : la quatrième étape disciplinée : la distillation de la connaissance qui fait référence à la recherche des valeurs essentielles qui offrent une intégralité unificatrice. Michael Schneider nous dit : « Les pythagoriciens ont réalisé que la Tétraktys représentait un ensemble, une unité, une synthèse de l’ensemble qui comprenait la complétude des mathématiques et les archétypes qui se manifestaient comme les formes visibles du monde. » John Michell écrit : « La Tétractys, la forme triangulaire du nombre 10, avait la même signification pour les pythagoriciens que le diagramme de l'Arbre de Vie dans la mystique juive (discuté dans l'article 6), tous deux étant considérés comme des symboles de l'univers, et les nombres 1 à 4 qui le composent étaient censés être à la racine de toute création. »
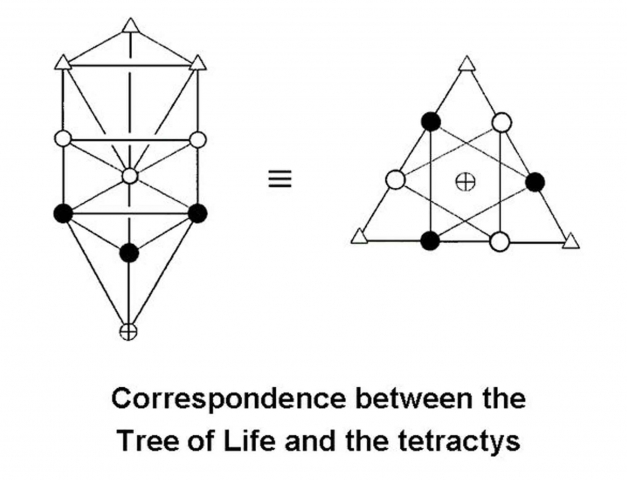
L'alphabet sacré des Pythagoriciens En guise de section bonus, j'inclurai une évaluation intéressante de l'alphabet sacré pythagoricien tel que décrit par Anne Macaulay dans Hommage à Pythagore – La définition pythagoricienne de Dieu. Macaulay écrit : « Les Pythagoriciens étaient uniques en ce sens qu'ils utilisaient les lettres de l'alphabet à la fois comme chiffres (une caractéristique commune à tous les premiers usages alphabétiques) et comme symbolisme géométrique. La géométrie sous la forme pythagoricienne bien connue est propre aux Pythagoriciens grecs, donc la réflexion suivante était de savoir si l'alphabet sous une forme sacrée pré-littéraire était à la racine de la culture mégalithique. Cette idée fait de l'alphabet un système numéro-géométrique qui était également utilisé pour les éléments de base du discours (voyelles et consonnes). S'il y avait eu une forme sacrée antérieure, alors elle n'aurait pas été utilisée pour écrire le langage vulgaire.
L'alphabet sacré est un système ancien dans lequel les chiffres et les éléments géométriques étaient représentés par des symboles géométriques ; à chacun de ces signes était ajouté un seul son (voyelle ou consonne), afin de créer des noms appropriés à leurs figures géométriques significatives. Nous évaluons ici le nom du dieu Apollon. Apollon représentait le principe transcendant. Cela contrastait avec Dionysos – le Principe divin dans sa genèse ou son devenir. Dionysos doit être déchiré en morceaux et sacrifié par les Titans, puis réassemblé et mémorisé. C'est Apollon – celui qui a été transformé A = un cercle de dix unités de diamètre (alpha = 1ère lettre) P = un cercle de 17 unités de circonférence (pi = 17e lettre) O = un cercle de 16 unités de circonférence (omicron = 16e lettre) L = un rectangle de 3 x 4 côtés (lambda = 12e lettre) N = un cercle de 14 unités de circonférence ; son diamètre est de 4,4545, en utilisant pi = 22/7 (nu = 14e lettre)




Les valeurs numéro - géométriques des lettres du nom Apollon forment une figure concise et bien définie. Ainsi, nous pouvons conclure qu’Apollon est le nom dérivé par l’alphabet numéro - géométrique sacré d’une figure géométrique, elle-même dérivée d’observations astronomiques des étoiles circumpolaires et de la lune. Les dimensions secondaires de la figure sont l’ensemble des proportions de l’échelle et les lois acoustiques de base.
Apollon, le dieu dérivé d’une figure géométrique, n’est ni un héros déifié ni une déité archétypale, mais une synthèse de faits observés sur la relation des étoiles, de la lune et du soleil à la terre ; c’est une horloge et un calendrier ; c’est une déclaration des lois du ciel en termes d’éléments géométriques et mathématiques qui présentent eux-mêmes des lois absolues ; et ces lois s’appliquent également à la musique.
L’existence de ce courant de sagesse d’Apollon explique le problème de savoir pourquoi les enseignants ultérieurs, Socrate et Platon, etc. étaient connus comme pythagoriciens à leur époque, mais il n’y avait pas d’intermédiaire direct qui aurait pu leur transmettre l’enseignement de Pythagore. Le lien est qu’ils enseignaient tous en public des aspects de la sagesse d’Apollon.
Le message le plus important qu’Apollon nous adresse aujourd’hui est peut-être de reprendre conscience dans la pratique de l’harmonie qui imprègne tout être.